probability
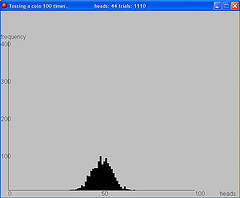
Demonstrates coin tossing, dice tossing, bar graph of cumulative heads and tails, approximation of a normal distribution from repeated sets of 100 tosses
acceleration, speed, position, sum of series, medium level violence (to frogs)
1/2 + 1/4 + 1/8 approaches 1
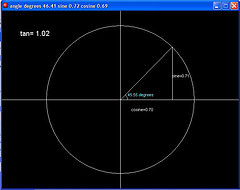
sin, cos, tan and their uses
An explanation of trigonometric functions and 4 game samples using them (GM5.3a)

newton - Newton's law of gravity,
or
newton1 - drop into lunar orbit (a bit more complicated)
Newton published his famous law of universal gravitation in his Principia Mathematica in 1687 as follows:
F = G x m1 x m2
______________________________
r²
In this demonstration, an initial speed of 5 is used to escape the Earth's gravity and a further deceleration to speed 1after 40 steps is required to drop into lunar orbit.
Lunar lander,
Suggestions for improving
this game:
Sprites for lander with side rockets when firing; keyboard left & right
event: change sprite, hspeed= +- value relative; fuel bar showing
remaining fuel, no fuel means no rockets; rough terrain, collision event
= failure; smooth terrain, collision event = success, if hspeed< value
&& vspeed <value; display hspeed and vspeed in menu bar
improve the title screen
Is the physics correct? The lander rocket applies a force F; F=MA; A =
change in velocity/time; if the force of the rocket and the mass are
constant, firing the rocket produces a change in velocity for each time
step. There is no atmosphere and no friction.
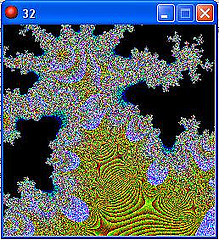
Fractals (GM5)
Fractals (GM6)
The Mandelbrot set is defined by the iterative recalculation of:
z = z² + c
where z and c are complex numbers, made up of a real part x and an imaginary part iy where i is the square root of -1.
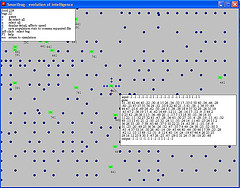
Simulation genetics, natural selection and population dynamics, export to spreadsheet (GM5)
" (GM6)
See how badly adapted lifeforms become extinct:
The first to die are the ones that don't move
Soon they are all related through one ancestor
Diagonal movers take over from horizontal and vertical movers
They learn to spread out
Some get stuck with some food patterns and die
Eventually the learn to hunt for food
What angle should you throw a ball to get maximum range?
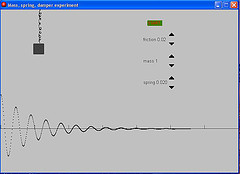
Mass spring damper experiment with graphing function - resonant frequency, critical damping etc. (GM6)
For the mass: F = ma
For the spring: F = springconstant x distance
For the damper: F = frict x speed
So: a = (springconstant x distancestretched + frict
x speed)/m
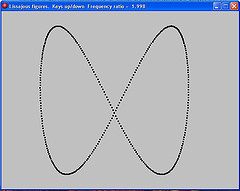
Lissajous curves are the family of curves described by the equations:
x(t) = sin(w1 * t + d1)
y(t) = sin(w2 * t + d2)
Where w1 and w2 are the frequencies of the x and y axes. They were studied by Jules-Antoine Lissajous in 1857. Lissajous curves have applications in physics, astronomy, and other sciences.
(GM6)
You can just have fun with this adding more levels or you can use it to investigate potential and kinetic energy. (GM6)
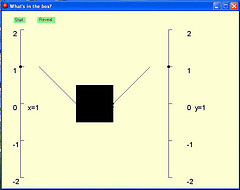
Move the x lever up and down with the mouse. See what's happening to the y lever. Guess what's in the box. Press reveal when you know what's in the box. Press start to get a new puzzle.
The box contains a random formula of the form y = a + b*func(x)
Challenge: add new functions and constants
dn = 1
____________
1-cos( 2pi/n)
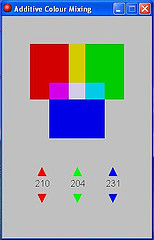
Click on the up/down arrows to change the colour mix
Challenges:
Reprogram for subtractive colour: cyan/yellow/magenta
Make the colours vary with time, for example, use the sine function.
Make the colours vary with music, different colours for high, mid or low tones
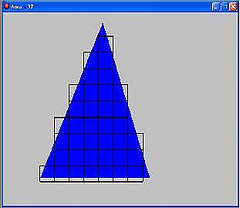
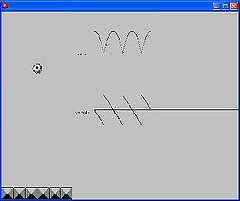
Graphed position and
velocity for a bouncing ball
You can move the ball by clicking and dragging
Challenges:
Add friction in motion (air drag)
To correctly model air drag, what is the formula?
Add friction on bouncing
Graph the acceleration, what units is it in? What happens when it
bounces?
Graph potential energy (mgh) and kinetic energy (1/2mv²) on the same
axes
What is m?
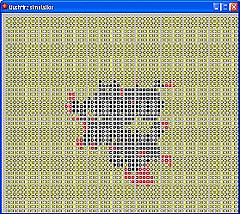
Bushfire simulation
Enter the probability (0-100%) of a tree igniting each of its four
neighbours
mouse click on a tree to start.
Challenges
Take into account the effects of wind direction and temperature
Allow fire fighting and back-burning

Rotate with right mouse
Drag to bin to destroy

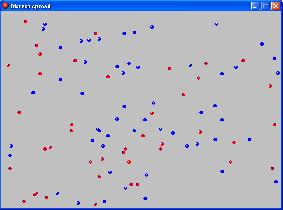
Demonstration of clustering by 2 populations
The controller fills the room with random red and blue balls and some blank space
For red and blue objects, they will stay put if they are near their own colour but not if they are near the other colour
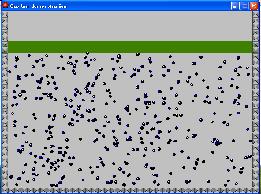
When an infected ball collides with another it infects it:

The scent trails are made stronger by the ants, the ants turn towards a scent trail
Left and right side collisions are sensed by cycling the sprite: whole ant/ left feeler/ right feeler also the multi image sprite is rotated to match the direction the ant is moving
Then the ant is turned depending on which feeler contacted scent
P is the absolute pressure of the gas, V is the volume of the gas, n is the number of moles of gas, R is the universal gas constant, T is the absolute temperature.