Learning Objects - open source T

Learning Objects - open source
These learning objects are based on the idea that multiple representations of a concept help understanding. They can be just run as simulations or can be modified and experimented with by changing the source code. Putting it more simply, you can "look at the engine and kick the tyres".

They are the endpoint of a continum from animated demonstrations which can be observed but not altered, through virtual manipulatives which can be altered in predefined ways through to open source objects which can be observed, manipulated or totally reprogrammed. For more discussion of these ideas see Multimedia Learning in Games, Simulations, and Microworlds

I have chosen to program these open source objects in Gamemaker for two reasons:

Gamemaker is well suited to graphical representations of moving objects
It is an easy language for students to master via game creation

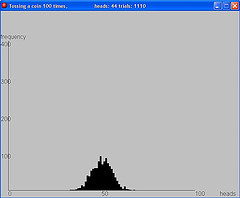
	dice.gmd dice.exe	probability Demonstrates coin tossing, dice tossing, bar graph of cumulative heads and tails, approximation of a normal distribution from repeated sets of 100 tosses
	frogjump.gmd frogjump.exe	acceleration, speed, position, sum of series, medium level violence (to frogs) 1/2 + 1/4 + 1/8 approaches 1
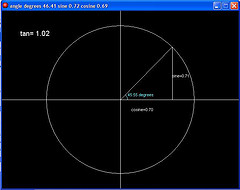
	trig53a.gmd trig53a.exe	sin, cos, tan and their uses An explanation of trigonometric functions and 4 game samples using them (GM5.3a)
	newton.gmd newton.exe newton1.gmd newton1.exe	newton - Newton's law of gravity, or newton1 - drop into lunar orbit (a bit more complicated) Newton published his famous law of universal gravitation in his Principia Mathematica in 1687 as follows: F = G x m1 x m2 ______________________________ r² In this demonstration, an initial speed of 5 is used to escape the Earth's gravity and a further deceleration to speed 1after 40 steps is required to drop into lunar orbit.
	lander.gmd lander.exe	Lunar lander, Suggestions for improving this game: Sprites for lander with side rockets when firing; keyboard left & right event: change sprite, hspeed= +- value relative; fuel bar showing remaining fuel, no fuel means no rockets; rough terrain, collision event = failure; smooth terrain, collision event = success, if hspeed< value && vspeed <value; display hspeed and vspeed in menu bar improve the title screen Is the physics correct? The lander rocket applies a force F; F=MA; A = change in velocity/time; if the force of the rocket and the mass are constant, firing the rocket produces a change in velocity for each time step. There is no atmosphere and no friction.
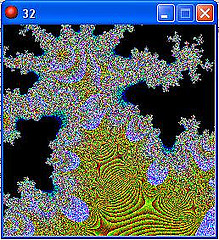
	fractal.gmd fractal.gm6 fractal.exe	Fractals (GM5) Fractals (GM6) The Mandelbrot set is defined by the iterative recalculation of: z = z² + c where z and c are complex numbers, made up of a real part x and an imaginary part iy where i is the square root of -1.
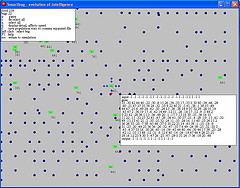
	smartbug1.gmd smartbug1.gm6 smartbug1.exe	Simulation genetics, natural selection and population dynamics, export to spreadsheet (GM5) " (GM6) See how badly adapted lifeforms become extinct: The first to die are the ones that don't move Soon they are all related through one ancestor Diagonal movers take over from horizontal and vertical movers They learn to spread out Some get stuck with some food patterns and die Eventually the learn to hunt for food
	throwing.gmd throwing.exe	What angle should you throw a ball to get maximum range?
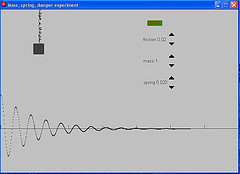
	mass-spring.gm6 mass-spring.exe	Mass spring damper experiment with graphing function - resonant frequency, critical damping etc. (GM6) For the mass: F = ma For the spring: F = springconstant x distance For the damper: F = frict x speed So: a = (springconstant x distancestretched + frict x speed)/m
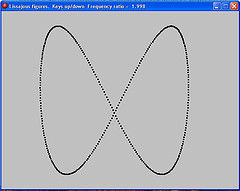
	pythagoras.gm6 pythagoras.exe	Demonstration of Pythagoras' theorem (not a proof) drag the triangle apex with the mouse (GM6)
	lissajous.gm6 lissajous.exe	Lissajous curves are the family of curves described by the equations: x(t) = sin(w1 * t + d1) y(t) = sin(w2 * t + d2) Where w1 and w2 are the frequencies of the x and y axes. They were studied by Jules-Antoine Lissajous in 1857. Lissajous curves have applications in physics, astronomy, and other sciences. (GM6)
	moire.gm6 moire.exe	Demonstration of Moire Pattern from 2 circular screens. Suggestions of more things to try (GM6)
	superball.gm6 superball.exe	The demonstration is based on the conservation of energy. As a ball rolls down a lossless ramp, it converts its potential energy (mgh) into kinetic energy (1/2mv²). You can just have fun with this adding more levels or you can use it to investigate potential and kinetic energy. (GM6)
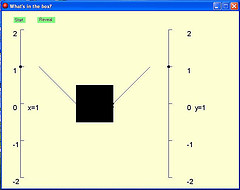
	whatsinthebox.gm6 whatsinthebox.exe	What's in the box? A maths guessing game (GM6) Move the x lever up and down with the mouse. See what's happening to the y lever. Guess what's in the box. Press reveal when you know what's in the box. Press start to get a new puzzle. The box contains a random formula of the form y = a + b*func(x) Challenge: add new functions and constants
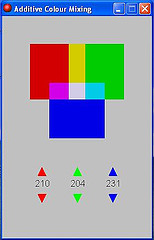
	mouse.gm6 mouse.exe	In the mice problem, also called the beetle problem, n mice start at the corners of a regular n-gon of unit side length, each heading towards its closest neighboring mouse in a counterclockwise direction at constant speed. The mice each trace out a logarithmic spiral, meet in the center of the polygon and travel a distance d_n = 1 ____________ 1-cos( 2pi/n) From http://mathworld.wolfram.com/MiceProblem.html
	colour.gm6 colour.exe	Additive colour mixing. The colours that the human eye can perceive can be produced by the mixture of red, green and blue light. The eye has 3 kinds of receptors or cones sensitive to these colours. Computer monitors produce colour by the mixture of these colours. Click on the up/down arrows to change the colour mix Challenges: Reprogram for subtractive colour: cyan/yellow/magenta Make the colours vary with time, for example, use the sine function. Make the colours vary with music, different colours for high, mid or low tones
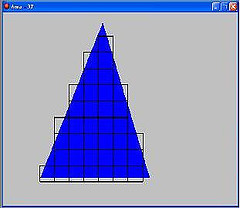
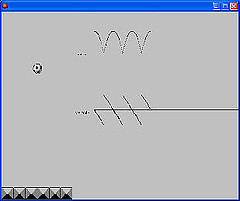
	triangle.gm6 triangle.exe	The area of a triangle is half base x height
	speed_acceleration.gm6 speed_acceleration.exe	Graphed position and velocity for a bouncing ball You can move the ball by clicking and dragging Challenges: Add friction in motion (air drag) To correctly model air drag, what is the formula? Add friction on bouncing Graph the acceleration, what units is it in? What happens when it bounces? Graph potential energy (mgh) and kinetic energy (1/2mv²) on the same axes What is m?
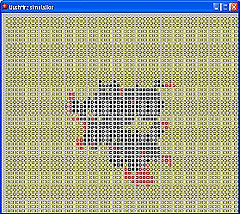
	fire.gm6 fire.exe	Bushfire simulation Enter the probability (0-100%) of a tree igniting each of its four neighbours mouse click on a tree to start. Challenges Take into account the effects of wind direction and temperature Allow fire fighting and back-burning
	rectangles.gm6 rectangles.exe	Drag rectangles with left mouse Rotate with right mouse Drag to bin to destroy
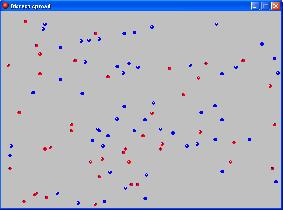
	seggregation.gm6	Demonstration of clustering by 2 populations The controller fills the room with random red and blue balls and some blank space For red and blue objects, they will stay put if they are near their own colour but not if they are near the other colour
	disease.gm6	The controller fills the room with one red and some blue balls and some blank space When an infected ball collides with another it infects it:
	scentV2.gm6	Demonstration of of ant scent trails The scent trails are made stronger by the ants, the ants turn towards a scent trail Left and right side collisions are sensed by cycling the sprite: whole ant/ left feeler/ right feeler also the multi image sprite is rotated to match the direction the ant is moving Then the ant is turned depending on which feeler contacted scent
	fission.gm6	Nuclear fission chain reaction
	decay.gm6 decay.exe	Nuclear decay
	gaslaw.gmk (GM7) gaslaw.exe	The ideal gas law is the equation of state of a hypothetical ideal gas, The state of an amount of gas is determined by its pressure, volume, and temperature according to the equation: PV = nRT where P is the absolute pressure of the gas, V is the volume of the gas, n is the number of moles of gas, R is the universal gas constant, T is the absolute temperature.
	diffusion.gmk (GM7)	Diffusion